Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique

Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique Ecole Nationale Polytechnique de Yaoundé

Problème 1

Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique: On réalise la combustion complète de 2 moles de butène

1. Donner la formule développée de ce corps, \Rightarrow dire à quelle famille d’hydrocarbures il appartient, \Rightarrow dire quelle isométrie il présente et \Rightarrow donner les formules des différentes isomères en les nommant.
2. Ecrire l’équation équilibrée de la réacton et calculer le volume de vapeur d’eau produite mesurée dans les conditions normales (volume molaire = 22,4 litres .
3. La totalité du gaz carbonique recueilli trouble l’eau de chaux. Calculez la masse de carbonate de calcium formée. kamerpower.com

C = 12 g       H = 1 g     O = 16 g    Ca = 40 g

---

Solution au problème 1 

1) Formules développées du butène C₄H₈ 

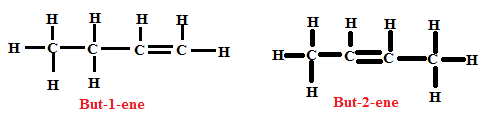
• Il s’agit d’un alcène.
• Il présente une isométrie de chaine.
• Et autre isomètre

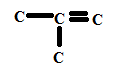
2)  Equaion:

C4H8 + 6O2 => 4CO2 + 4H2O

nC4H8 = nH2O/4 => VH2O/Vm  = 4nC4H8

VH2O = 4VM.nC4H8  => VH2O = 4×22,4×2 = 179,2

3) la masse de carbonate de calcium formée:

équation:  

CO2 + CaO => CaCO3

nCO2 = nCaCO3 => nCO2 = nC4H8

(mCaCO3/MCaCO3) =  4nC4H8

mCaCO = 4MCaCO3.nC4H8

mCaCO3 = 0.8kg

Problème 2 – Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique

Un électron pénètre entre les plaques d’un condensateur à égale distance des deux plaques distantes de h = 1 cm et soumises à une d.d.p de 200V avec une vitesse initiale parallèle aux plaques  v = 50 000 km/s

1. Sachant que les plaques du condensateur mesurent chacune 5 cm de longueur, calculez l’ordonnée  y_M de l’électron juste à la sortie du condensateur
2. Un écran fluorescent est placé à une distance d = 20 cm du condensateur, calculez l’ordonnée y_E de l’impact de l’électron sur  l’écran.   e = 1,6.10^{-19 C}    ,   m_e =0,9.10^-30  kg

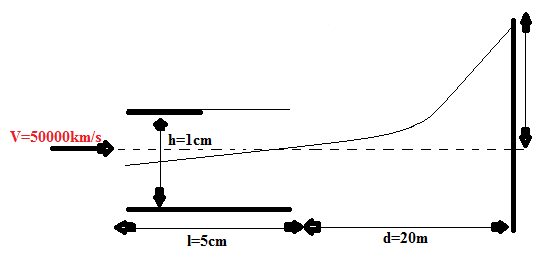
Solution au problème 2 – Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique

1)  Le principe fondamental de la dynamique donne

En projetant sur les axes on a   mx = 0  , my = eE  et mz = 0

x = 0  \Rightarrow x = v \Rightarrow x = vt ——(1)

y=\frac{eE}{m} \Rightarrow y=\frac{eE}{m}t    \Rightarrow

Y = (eE/2m)/t^2  ———-(2)

t=\frac{x}{v} \Rightarrow

Y = (eE/2mv^2)/x^2

Pour x = l  et E=\frac{U}{h},  on a  

YM = (eU/2mhv^2)l2

Donc :

TM = [(1,6.10^-19) x 200 x (25.10^-4)] /  2x(0,9.10^-3)x(10^-2)x2,5.10^-4)

YM = 1,77×10^-3m

2)  Calcul de Y_E

En sortent V_{{S}}:

Vx = V,  vy = (eE/m)ts  = (eEl/mv)ts, vz =0

la déviation est

tga = vy/vy  = (eEl/mv^2)

YE =  [eUl(l/2 + d)]/ mv^2 h

YE = 1,6m

Sujet Corrigé Concours ENSP Yaounde 2013 Chimie et Physique Ecole Nationale Polytechnique de Yaoundé

---

Evenements Concours lances 2026-2027: